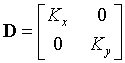
La modelización del comportamiento de muchos fenómenos naturales puede describirse utilizando la formulación diferencial cuasi armónica conocida en el argot matemático como la ecuación de Poisson.

Dicha ecuación puede modelar, entre otros problemas, el mecanismo de conducción de calor a través de un cuerpo, o bien, el flujo de un líquido en un medio permeable. En un siguiente apartado se dará una descripción de los diversos fenómenos naturales que rige esta ecuación, así como la equivalencia de las variables usadas. Sin embargo, para poder dar un significado tangible a la descripción de las ecuaciones que se utilizarán, se ha tomado como ejemplo concreto el problema de la conducción de calor, ya que se puede considerar como la aplicación más sencilla y generalizada.

La ecuación de Poisson estacionaria para un dominio bidimensional puede expresarse en la forma siguiente:

D Ñ ²f + Q = 0 en W

En donde f representa la temperatura, Q la densidad por fuente de calor interno: D corresponde a la matriz constitutiva, formada por las conductividades térmicas, K, paras las distintas dimensiones en que se describe el dominio W; de esta manera para un dominio bidimensional corresponde a:

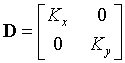
Alternativamente D quedará descrita para los casos uni y tridimensional como:

Caso unidimensional

Caso tridimensional

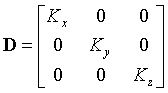
Las condiciones de contorno a las que se encuentra sujeta la formulación anterior se esquematizan en la siguiente figura, y son conocidas en términos matemáticos como las condiciones de

1. Dirichlet: Determina la temperatura f, a un valor fijo y conocido de antemano sobre un contorno particular.
2. Neumann: Determina el gradiente de la temperatura normal a la superficie.

En las ecuaciones anteriores es la temperatura con valor conocido en la frontera, a representa al coeficiente de convección - radiación, es el flujo o gradiente de la temperatura, con valor conocido en la frontera, f_ext es la temperatura en el exterior del dominio, mientras que el resto de las variables quedan definidas con las siguientes expresiones:

Vector de normales al contorno:

Vector de gradientes de la temperatura:

En donde el gradiente corresponde a:

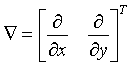
Resulta inmediato la expresión de las ecuaciones anteriores para los caos uni y tridimensionales, por lo que se omiten sus desarrollos.

Dependiendo de los valores escogidos para los parámetros de la ecuación asociada a la condición de contorno de Neumann, es posible reproducir los siguientes casos en el contorno:

1. Contorno aislante. Matemáticamente conocido como la condición de Neumann o condición de contorno natural que representa un flujo de temperatura cero en la interface del dominio con el medio circundante, de manera que:

por lo que y a

 

 

2. Contorno con pérdida o aporte de flujo externo. La condición señalada queda representada matemáticamente por:

por lo que a

 

3. Contorno con pérdida o aporte de calor por convección – radiación. En este caso existe una interacción del calor existente en el medio exterior f_ext y la temperatura del dominio f que de acuerdo con las leyes de la termodinámica se presentara un flujo en la interface representado por:

Como se ha mencionado en párrafos anteriores, los términos de las ecuaciones antes mostradas tienen diferentes significados físicos, dependiendo del problema que se modelice, A continuación se listan algunos de los casos que son más comunes.