ABSTRACT

In this work, we propose a convex, finite-dimensional and exact relaxation for non-convex, one- dimensional, variational problems given as: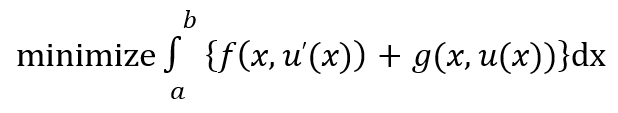




where the function 𝑓 is a pretty general rational function in the derivative 𝑢′ and the function 𝑔 is a linear expression in the admissible function 𝑢. These problems may have a solution in particular Sobolev spaces, in spite of its non-linear and non-convex nature. We analyze them by using Young measure's techniques to understand the precise behavior of its minimizing sequences and the features of its minimizing functions.

We apply here a change of measure in the Young measure's variational formulation, so that we can express them as a linear combination of its algebraic moments, connected with the polynomial in the numerator of the rational function 𝑓. In this way, we obtain a finite dimensional, convex, optimal control problem, solvable by a proper combination of numerical analysis tools taken from the Finite Element Method and Semidefinite Programming Algorithms, extensively used in optimization.

At last, we succeed obtaining an exact, finite dimensional and convex relaxation for a wide family of highly non-linear, non-convex, one-dimensional variational problems and we succeed in calculating numerically their optimal solution inside the proper Sobolev space, whenever it exists. Incidentally, our method is a good technique to prove the existence of minimizers in such non-convex, non-linear problems.

Finally, we show how this method is a strong and optimistic approach to analyze and solve non- linear problems arising in one-dimensional elasticity by combining techniques of FEM and non- convex optimization.

SPEAKER CV

René Meziat is a holder of a Mathematics degree from Universidad de los Andes, Bogotá, and a Ph.D. in Mathematics from the Technical University of Catalonia, Barcelona, with his thesis "Variational Problems, Optimization, and Control Theory" under the mentorship of various esteemed professors. Over the span of his career, he has been a part of the faculty at several institutions, including Universidad de Castilla la Mancha, Spain, and Universidad de los Andes, Bogotá, during which he has contributed to over 100 academic articles and led the scientific and technical aspects of numerous research projects. He collaborates with various research groups to enhance the scientific and technical aspects of project proposals, while also exploring the impact of Open Science policies at international, national, and regional levels. René also serves as the lead for several projects, demonstrating his leadership and coordination skills. In addition to his primary roles, Dr. Meziat also collaborates with various universities as an associate lecturer, sharing his wealth of knowledge with the next generation of mathematicians.