PFEM-2
The Particle Finite Element Method-Second Generation (PFEM-2) is an alternative PFEM technique to solve the incompressible Navier-Stokes problem with large time steps. The method was presented very recently in [1]. The key idea of the method is based on coupling the standard PFEM with the X-IVAS (eXplicit Integration following the Velocity and Acceleration Streamlines) method, which consists of integrating the convective terms following the streamlines rather than the particle trajectories.
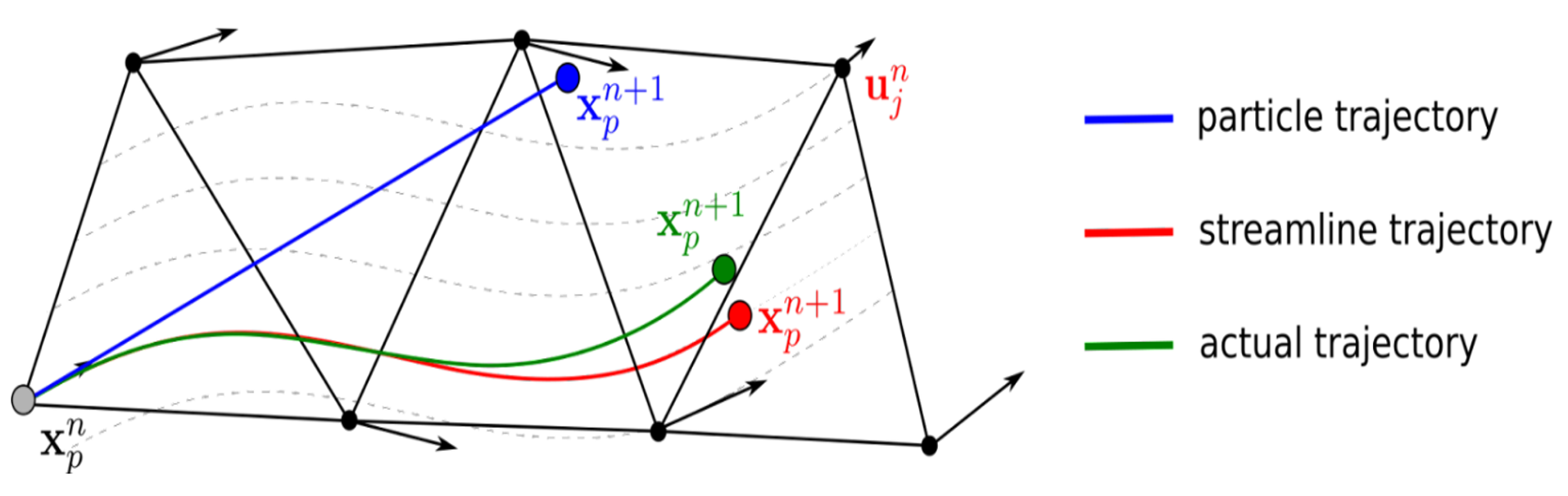
Different approximations of the actual trajectory of a fluid representative volume.
Two different versions of PFEM-2 have been proposed so far. The first one, the PFEM-2 with moving mesh, is based on the standard PFEM scheme and it creates a new mesh using the position of the nodes. Conversely, in the PFEM-2 with fixed mesh, the initial background mesh is kept unchanged during the analysis and the information is mapped on this fixed mesh. The first technique needs to re-build the mesh when is too distorted, as it happens in standard PFEM, and it is very efficient for free-surface flows. The approach with fixed mesh, on the contrary, maps the variables on the mesh avoiding the generation of a new one, and it is particularly suited for fluid flow problems in closed domains [13].

Left: PFEM-2 with moving mesh. Right: PFEM-2 with fixed mesh.
PFEM-2 Simulation of the Rayleigh-Taylor instability at Atwood number 3. Comparison among simulations with different time-steps [4]
Experimental validation of PFEM-2. Case: collapse of a water column [4]
A series of combined-explicit implicit methods based on employing PFEM2 strategy in a fully Lagrangian framework (actually moving grid + virtually moving grid) was proposed in [11,12]. The methodology allowed obtaining effecient schemes not bound by severe time step limitations and, at the same time, characterized by second-order accuracy in time [11,12].
An interesting feature of PFEM-2 is the possibility to use an explicit time integration independently on the Courant number. The method remains explicit and stable independently on the mesh size. The time step is established following only accuracy considerations, besides the limits given by the Fourier number. In [10] a second-order accurate in time and space formulation showed drastic computing times savings regarding standard Eulerian alternatives.
Injection of a liquid jet in a chamber with PFEM-2. Tracking of the main core and primary atomization [7]
The PFEM-2 has been applied successfully to different engineering problems. In [3], the ideas presented in [1, 2] were generalized for multifluid flows with large time steps.
PFEM-2 simulation of the Rayleigh-Taylor instability at Atwood number 3 [4]
In [4], an extended validation of the method for academic problems is presented. Gimenez et al. [8] show the potential of PFEM-2 to simulate industrial problems of large time duration. An application of the method to jet atomization simulation can be found in [5]. Becker and Idelsohn [6] show the potential of PFEM-2 to simulate large scale landslides events. FSI problems are tackled with a monolithic PFEM-2 approach in [5]. Finally, [9] shows an application of the method to the simulation of sediment transport phenomena in rivers.
References
[1] Idelsohn SR, Nigro N, Limache A, Oñate E (2012) Large time-step explicit integration method for solving problems with dominant convection. Comput Methods Appl Mech Eng 217- 220:168–185
[2] Idelsohn SR, Nigro N, Gimenez J, Rossi R, Marti J (2013) A fast and accurate method to solve the incompressible Navier–Stokes equations. Eng Comput 30(2):197–222
[3] Idelsohn SR, Marti J, Becker P, Oñate E (2014) Analysis of multifluid flows with large time steps using the particle finite element method. Int J Numer Methods Fluids 75(9):621–644
[4] Gimenez JM, González LM (2015) An extended validation of the last generation of particle finite element method for free surface flows. J Comput Phys 284:186–205
[5] Becker P, Idelsohn SR, Oñate E (2015) A unified monolithic approach for multi-fluid flows and fluid–structure interaction using the particle finite element method with fixed mesh. Comput Mech 55(6):1091–1104
[6] Becker P, Idelsohn SR (2016) A multiresolution strategy for solving landslides using the particle finite element method. Acta Geotech 11(3):643–657
[7] Gimenez JM, Nigro NM, Idelsohn SR, Oñate E (2016) Surface tension problems solved with the particle finite element method using large time-steps. Comput Fluids 141:90–104
[8] Gimenez J, Ramajo D, Damián S, Nigro N, Idelsohn SR (2017) An assessment of the potential of PFEM-2 for solving long real-time industrial applications. Comput Part Mech 4(3):251–267
[9] Bravo R, Ortiz P, Idelsohn SR, Becker P (2019) Sediment transport problems by the particle finite element method (PFEM). Comput Part Mech 1–11
[10] J.M. Gimenez, H. Aguerre, S.R. Idelsohn, N. Nigro (2019). A second-order in time and space particle-based method to solve flow problems on arbitrary meshes, Journal of Computational Physics, 380: 295-310.
[11] Marti J., Ryzhakov P.B. (2020) An explicit–implicit finite element model for the numerical solution of incompressible Navier–Stokes equations on moving grids. Computer Methods in Applied Mechanics and Engineering 350, 750-765.
[12] Marti J., Ryzhakov P.B. (2020). Improving accuracy of the moving grid particle finite element method via a scheme based on Strang splitting, omputer Methods in Applied Mechanics and Engineering 369, 113212.
